У каждого из нас есть внутренне пространство, которое мы заполняем тем, чего просит душа. Один покоряет горные вершины, другой прыгает с парашютом, а вот доктор технических наук, профессор СГТУ Андрей Кочетков и исследователь Петр Федотов с нешуточным пылом ведут подкоп под бесспорные истины и незыблемые величины.
Занимаются они этим уже давно, действуя в глубоком арьергарде альтернативной научной мысли и препарируя как штампы школьных учебников, так и постулаты, возведенные в статус аксиом. И вот, разгребая пыль всяческих нетленок, саратовские физики сумели прийти к очень интересным выводам и даже предложить простые решения задач, там, где современная наука выбрала крайне сложный путь. О своих мыслях и находках ученые рассказали в нескольких книгах. Наш разговор о последней из них, вышедшей в 2019 году в столичном издательстве «Инновационное машиностроение», но и не только о ней.
«Теряют мелочь размером со слона»
- Начнем с традиционного вопроса: как все это началось? Вы оба, уважаемые, получили добротное советское образование, занялись наукой, причем в прикладном аспекте, где теория не отрывается от практики, но при этом все время держали фигу в кармане? Откуда эта страсть ерничать и сомневаться?
Андрей Кочетков: Вот именно потому, что мы оба прикладники, мы всю жизнь сталкиваемся с одной картиной: в школе на уроках физики учим одно, в вузе – на ту же тему нам говорят другое, а в практической жизни заявляют – забудьте все, чему вас там научили, потому что это не работает. Как же так? Почему законы, даже если они носят великие имена, не подтверждаются практикой? Тогда зачем такие законы нужны? Почему мы сначала их учим, запоминаем формулы, но практический вопрос, задачу из жизни по этим формулам не решить? Ответы же берутся из справочников, из таблиц с экспериментальными данными.
Петр Федотов: И это расхождение между школьной программой, вузовской физикой и реальной жизнью стало до того привычным, что никто вслух не задает неудобные вопросы. Ну, а мы решили задать. В книге «Маятник» рассматривается пример известной задачки про маятник, которую решает каждый школьник. Формулу вывел математик Гюйгенс еще в XVII веке, но – для малых колебаний. Для больших амплитуд задача теоретически была решена в XIX веке при помощи эллиптических интегралов. Чтобы постичь это решение, нужно с отличием окончить школу, затем с красным дипломом – физмат МГУ и еще лет 5 тренироваться в эллиптических интегралах.
- Где на практике применяются колебания большой амплитуды и как тогда выходят из положения?
А.К.: Все колебательные процессы в мире – маятниковые, колеблются планеты, двигаясь по своим орбитам, приливы и отливы – это колебания, вибрация деталей в станках - тоже. Как выходят из положения, если нужно рассчитать оптимальную частоту колебаний при бурении недр или если надо выяснить, как быстро износится станок из-за вибрации? Обращаются к справочникам, где значения выведены либо экспериментально, либо мощные компьютеры все посчитали в эллиптических интегралах. Но мы предложили простейшее решение. Если отказаться от необходимости иметь точное значение мгновенной скорости маятника в каждой точке траектории и воспользоваться средним значением скорости маятника за период, то необходимость в дифференциальных уравнениях отпадет. Если 
, то период больших колебаний маятника T определяется по формуле Кочеткова-Федотова:
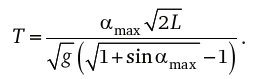В последней формуле приведено значение длины маятника L, как это принято в современной литературе, αmax - максимальный угол отклонения маятника.
С помощью этой формулы мы получаем точный результат - не методом последовательных приближений, не используя машино-часы суперкомпьютеров. С помощью этой формулы любой может сделать расчеты на калькуляторе, ее спокойно может применять даже школьник. Я не стану утверждать, что формула делает полностью ненужными дорогостоящие натурные эксперименты, но машино-часы компьютерных расчетов она исключает совершенно точно.
П.Ф.: У нас есть еще одна книга, вышедшая в том же издательстве, но в 2015 году – «Проблемы гармонизации радикальных противоречий в аксиоматике естественных наук». Там тоже есть примеры простого подхода к явлениям, которые науку почему-то ставят в тупик. Есть известная тема, которую проходят в школе, едва начинают изучать физику, – кинетическая энергия газов. Это как бы очень простой вопрос, на практике применение широчайшее – любой двигатель внутреннего сгорания, любая газовая турбина работают от того, что газ расширяется, движется и т.п. И при этом все пользуются эмпирическими значениями, добытыми опытным путем. Потому что на основе законов, принятых за истину, на основе официально утвержденных формул попадешь в бурелом. Значит, эти формулы что-то не учитывают, значит, есть какие-то факторы, из-за которых они не работают.
Возьмем еще одну совершенно рутинную тему, которую изучают шестиклассники, – броуновское движение. Мы знаем, что молекулы сталкиваются, по этой причине выделяется тепло. Чем больше тепла, тем интенсивнее броуновское движение и выше давление в емкости, где содержится газ. Это все описано в уравнении Менделеева-Клапейрона для идеального газа. Для реального газа уравнение составил физик Ван-Дер-Ваальс, который вывел, что молекулы не просто ударяются друг о друга, но и взаимодействуют на расстоянии, примерно как Солнце и Луна.
Уравнение стало более точным, но решать практические задачи на его основе я бы никому не посоветовал. Что сделали мы? Мы внесли уточнение, что тепло выделяется не от столкновения молекул, а от того, что атомы испускают фотоны. Но когда атом испускает эту частицу, он откатывается назад, как откатывается пушка, когда из нее вылетает ядро. А когда другой атом принимает эту частицу, он отлетает, потому что ловит импульс. Отсюда и броуновское движение. Казалось бы, ерунда, мелочь, но когда мы рассмотрели фотонное взаимодействие в тепловом аспекте и ввели этот фактор в уравнение Ван-Дер-Ваальса, точность расчетов выросла в четыре раза!
- То есть всегда, когда формулы расходятся с реальностью, дело в какой-то мелочи, которую не учли?
А.К.: Если бы так! Бывает, что теряют мелочь размером со слона! Вы знаете, что расчеты движения планет Солнечной системы по Птолемею дают погрешность в 2,5 часа за 54 года (в часах считается время прихода объекта в искомую точку), а если считать орбиты по законам Ньютона, то ошибка за тот же период составит 18 лет? При этом Птолемей - это замшелый реакционер, полагавший, что Солнце и все планеты вращаются вокруг земли, а законы Ньютона – это святыня, то, что сидит у всех нас в подкорке.
- А как считают сейчас? Почему самолеты не сбиваются с курса и корабли приплывают куда им положено?
А.К.: Все считают машины с использованием мощного математического аппарата, в то время как у Птолемея компьютера не было, и даже синуса с косинусом он не знал. А точность измерений у него была, причем за результаты европейские астрономы и астрологи, работавшие по его системе, отвечали головой. И навигационные приборы, разработанные на основе расчетов Птолемея, были точными, потому что если они ошибались, то голову могли отрубить уже королю. Плывет экспедиция за золотом в Вест-Индию, но не попадает в нужную гавань. Пять таких экспедиций - и казна пуста, а затем происходит революция, и короля тащат на плаху.
«Одна наука, и никаких попов»
- И как Птолемей в Древнем Риме так все точно считал, позвольте спросить?
А.К.: Он использовал механические системы зацепления зубчатых колес, соответствующих каждой естественной составляющей колебания. Современный аналог этому – расчеты по тригонометрическим функциям. Примерно такими же были навигаторы, которые веками применялись путешественниками на земле и на море для точного позиционирования. Расчеты делались, условно говоря, прутиком на песке, а сейчас подобной точности добиваются, используя мощнейшие компьютеры. При этом положения планет сейчас пересчитываются раз 20 лет, иначе накапливается погрешность.
- И это называется прогресс?
П.Ф.: Птолемея «свергли» в эпоху Просвещения, объявив, что он позавчерашний день, сумерки сознания, на том основании, что он ставил Землю в центр и считал, что Солнце и другие планеты вращаются вокруг нее, а как раз геоцентрической модели придерживалась церковь. А вот Ньютон это, наоборот, передовое, одна наука, и никаких попов. На самом деле законы Ньютона – это предельно упрощенный подход, а Просвещение в части навигационных расчетов – это, по нашему мнению, пиар и чистой воды провокация. Потом налетели на ошибку в 18 лет и по-тихому, неофициально, вернули Птолемея. На поверхности же бушевали бури, отвоевывала себе место в методах расчета гелиоцентрическая система. Это преподносилось как победа науки над церковью, разума над невежеством.
- То есть все это тоже пиар? А как же Галилео Галилей, который сначала каялся и отрекался, а потом чуть не шепотом сказал: «А все-таки она вертится» - имея в виду, что Земля вращается вокруг Солнца вопреки учению церкви?
П.Ф.: Это художественный вымысел, во-первых, а во-вторых, с точки зрения физики совершенно неважно, что в центре – Земля или Солнце. Возьмем задачку, которую решает любой школьник: я еду на поезде и нужно узнать с какой скоростью относительно поезда параллельно едет автомобиль. Удобно считать относительно себя, т.е. поставив в центр Землю, но можно пересчитать, поставив в центр Солнце, и ввести еще скорость движения Земли вокруг светила.
- То есть пафос вашего сочинения «Маятник» в том, чтобы вернуть Птолемея и его систему?
А.К.: Нет, пафос нашего сочинения в том, чтобы вернуть то правильное и эффективное, что было незаслуженно отброшено, заслонено модными когда-то веяниями. В эпоху Просвещения силу набирала новая идеология и ей нужны были новые имена и авторитеты в противовес тем, которые она сбросила с корабля. И что мы имеем сегодня? Вот вы спросили, как Птолемею удавалось так точно считать? Почему сегодня при расчете волновых колебаний применяется регулярный гармонический анализ, который при котором погрешность возникает на пятой гармонике, а у Птолемея погрешность те самые 2,5 часа за 54 года? Потому что он анализировал явления природы и применял естественный, а не регулярный гармонический анализ, и считал по естественным координатам. А у нас применяют регулярный гармонический анализ с произвольно заданной постоянной регулярностью, потом применяется метод подбора, но все равно требуемой точности достичь не удается.
Птолемей не знал синуса, косинуса, но на своих зубчатых колесах он строил то, что называется тригонометрической аппроксимацией, а у нас применяется аппроксимация степенная, у нее погрешность резко больше. Полиномы Чебышева и функции Бесселя, описывающие волновые процессы, работают хорошо только для машин с заданными регулярными параметрами, но не могут работать оптимально для естественных колебаний, которые характерны для природы, живой материи. В этих случаях возникает неустранимая погрешность, но мы нашли метод, как применить гармонический анализ для естественных циклов.
«Молчи и вычисляй»
- А зачем, по большому счету? Сейчас все эти заморочки с регулярностью, с естественными ритмами устраняют машинные расчеты, корабли плавают по компасу, машины ездят по навигатору. В космос, как-никак летаем, спутники запускаем полвека уже.
П.Ф.: А затем, что если не решать эти задачки, то пробелы, допущения и неработающие законы достигнут критической массы. Уже сегодня мы живем в парадигме научной веры, наука по большому счету не может объяснить, чем же она занимается. А все потому, что после первого наступил второй этап просветительской деятельности. Ньютона точно так же скинули с корабля. Пришли Нильс Бор, Альберт Эйнштейн и другие молодые физики и сказали, что теперь они самые великие физики в мире. Это как революция: чтобы стать первым, нужно сбросить того, кто сейчас на троне. Механику Ньютона объявили ошибочной и отсталой, а квантовую механику – истинной и передовой. Были огромные сражения, молодые физики провели пять съездов, прежде чем одолели «ретроградов». На наш взгляд, это все имидж и маркетинг, а к науке это не имеет прямого отношения.
- Слушайте, даже я, сугубый гуманитарий, помню из школьного курса про фотопластинку, на которой оставляют след частицы. Законы Ньютона не позволяют даже близко вычислить, где будет этот след, а квантовая механика допускает некое облако вероятности и тем самым достаточно точно отвечает на вопрос.
А.К.: Безусловно, отвечает. Квантовая теория обогатила мир набором формул, которые работают, но почему – неясно. Их словно небо послало. Классическая, ньютоновская физика стройна и понятна, в ней все логически объясняется. В квантовой теории объяснение одно: вот тебе набор формул – молчи и вычисляй. Механика Ньютона перестала развиваться и не могла решить некоторые задачи, а квантовая может, но непонятным образом.
П.Ф.: Если бы эти наития шли косяком и дальше, если бы небо посылало все новые формулы… Но уже лет 70 ничего не посылает, и квантовая физика превратилась в научную веру. Прими эти скрижали, иначе тупо не сдашь экзамен и в вузе на следующий курс не перейдешь. Но мы уже не студенты, а взрослые люди, мы занимаемся наукой, у нас с логикой пока все в порядке. И если какие-то вещи мы 40 лет понять не можем, значит, нам либо плохо объясняют, либо просто обманывают. Поэтому мы и начали искать и обнаружили серьезные пробелы даже в темах из школьного курса. Мы просто не стесняемся задавать очевидные вопросы и ищем на них ответы, вот и все.
- Я что-то вот не слышала бурных баталий вокруг квантовой физики, никто ее с пьедестала не сбрасывает, ее постулаты формируют картину мира, как когда-то физика Птолемея формировала или физика Ньютона.
А.К.: Но при этом непонятно, откуда взялись эти постулаты, из чего они выведены. Мы ведь не призываем изгнать эту физику, мы говорим, что уже ясно виден ее предел, что есть вещи, которые квантовая теория объяснить не может, и есть вещи, которые прекрасно и логично объясняются без квантовой теории. Задача про маятник для больших амплитуд решена без квантовой механики. Через это решение мы выходим на задачи для небесных тел и для движения электрона, перехода его с орбиты на орбиту. Это уже квантовый эффект, но мы его рассчитываем без квантовой теории.
П.Ф.: Мы говорим, что нужно вспомнить Птолемея, но это не значит, что мы какие-то фанатики глубокой древности, призываем тут ввести в физику догмат о непорочном зачатии! И совершенно мы не говорим о том, что нужно отказаться от полиномов Чебышева, эллиптического интеграла или функций Бесселя. Она работают в своих областях – и это прекрасно. Мы лишь предлагаем с точки зрения здравого смысла посмотреть на некоторые постулаты квантовой теории, иначе так и будем принимать на веру, что нужно доверяться случайности, что наблюдаемое зависит от наблюдателя, а частица обладает свободой воли и интеллекта и сама выбирает себе для взаимодействия другую частицу.
- Мир уже в курсе того, что вы решили задачу маятника для больших колебаний?
А.К.: Перед тем, как вышла книга, была опубликована в издательстве «Машиностроение» в 2015 году монография «Проблемы гармонизации радикальных противоречий в аксиоматике естественных наук». Без этой публикации «Инновационное машиностроение» (так оно сейчас называется) не опубликовало бы «Маятник». Эта монография лежит в открытом доступе, примерно раз в три месяца я получаю запросы с просьбой ее выслать, так как у кого-то файл не раскрывается. Да, читают, интересуются. Ко мне даже студенты СГТУ подходили, где я преподаю.
П.Ф.: «Маятник» - сбалансированное произведение, там процентов 95 – это описание существующих подходов и новых способов решения задач механики маятника. Вот «Проблемы гармонизации...» - очень радикальная книга. Она была разослана по обязательной рассылке, ее заказали многие вузы. Но – ни одного официального отклика, положительного либо разгромного, не было.
- Почему?
А.К.: В научном мире есть своя иерархия, и вдруг появляются какие-то двое из Саратова, замахиваются на святое. При этом легко опровергнуть их нельзя, и формулы, которые приводятся, подтверждены экспериментально либо аппроксимации получены из реальных физических данных.
«Маятник» важен еще и в том плане, что это свидетельство нашей состоятельности и нашего права делать обоснованные заявления. Еще в начале 2000-х мы выпустили книжку, где полемизировали с Ньютоном и Эйнштейном, так что подкоп под научную веру мы ведем давно.
Мы в самой первой книге написали, что все нерешенные задачи сегодняшней науки имеют корни в истории. Мы ведь занимаемся этим не ради эпатажа, а потому что считаем, что непредвзятый подход и добросовестное критическое исследование приносят со временем значимые научные результаты.
Вопросы задавала Наталья Левенец.
